FUNCIÓN DE 2DO. GRADO

Todas las funciones de segundo grado o también llamadas cuadráticas con la variable "X" se puede representar de la siguiente manera representa así:

Donde a, b, c son numero reales, esto quieres decir que todos los números son diferentes a 0: 

Las funciones de segundo grado tienen las siguientes características:

 >Su representación en un plano real es con una "parábola".

 >El dominio es el conjunto de los reales, a no ser que se indique lo contrario.

 >La imagen es un subconjunto de los número reales y depende de los valores de a, b, c. 

La igualdad y= ax2 + bx + c es la ecuación de la parábola donde 

 >a es el coeficiente deltermino cuadratico

 >b es el coeficiente del l termino simple

 >c se le denomina termino independiente 

Para realizar este tipo de funciones es necesario seguir este esquema de trabajo muy claro que implica realizar en este orden, el estudio de los siguientes puntos  que les explicaremos en forma simple.

 > Concavidad 

En palabras sencillas es determinar cómo será la curvatura de la parábola. Se condiciona a saber el signo del coeficiente del término de segundo grado, que habitualmente llamamos a.

 - Si a > 0 la función tiene concavidad positiva, y decimos que “sonríe” aludiendo a que la parábola que la representa parece una sonrisa 

 - Si a < 0 la función tiene concavidad negativa y decimos que “está enojada” aludiendo a que la parábola parece una mueca de enojo.

La siguiente imagen nos muestra un ejemplo de concavidad positiva:

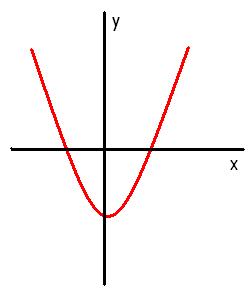
 > Ordenada al origen

Al calcular la ordenada al origen, estamos señalando el punto de corte con el eje de las ordenadas o eje vertical. La encuentras sustituyendo por 0  las x que veas en la expresión de la función, lo que comúnmente se conoce como “anular x”.

 > Raíces o soluciones

Revelan el o los puntos de corte del gráfico de la función con el eje horizontal o de las abscisas. Las calculas convirtiendo la función en una ecuación igualándola a cero, y resolviéndola. Esa o esas soluciones que podrían ser iguales entre sí o incluso no existir, son los puntos de corte que estás buscando.

 > Vértice

Representa el punto más “alto” de la curva si ésta tiene concavidad negativa  o el punto mas “bajo” si es una curva con concavidad positiva.

Al buscar el vértice lo que estás buscando es un punto, y por tato lo que buscas son sus coordenadas para ubicarlo en el plano. La coordenada x del vértice se halla con la fórmula        Vx= -b /2a; la coordenada y se halla sustituyendo ése valor de Vx que hallaste antes, en cada lugar donde aparezca x en la expresión de la función; el resultado es la coordenada “y” del vértice.

A continuación le pondré una dirección electrónica que los enviara a un ejercicio para poder revisar a manera mas experimental y más certera como es que se maneja y resuelve una función: 

https://www.geogebra.org/m/tEw3a5yc